Le populisme est-il possible?

Entendu comme un régime politique où le peuple gouverne, le populisme semble en croissance dans plusieurs pays. Pourtant, les opinions à son sujet ignorent souvent une question fondamentale : qui est le peuple? Depuis un demi-siècle, les économistes et politologues ont démontré que le peuple en tant qu’acteur gouvernant n’existe pas. D’apparence théorique ou abstraite, la question comporte des implications pratiques majeures quant à l’interprétation des résultats d’élection ou de référendum(1).
En réalité, le peuple n’existe pas sinon comme collection d’individus avec des préférences et des valeurs différentes. Les questions sont rares où l’on peut présumer de l’unanimité de tous ces individus (un minimum d’ordre public, par exemple). Sur des questions comme la quantité d’automobiles ou de lait à produire, ou encore de la répartition des revenus, peu d’individus partagent la même opinion.
En pratique, dire que le peuple doit gouverner revient nécessairement à dire qu’une partie du peuple en gouvernera une autre dont les préférences et les valeurs seront ignorées.
L’INSAISISSABLE VOLONTÉ DU PEUPLE
Les individus qui composent le peuple peuvent bien sûr gouverner sous la forme d’une majorité électorale ou référendaire. Il a toutefois été démontré que les résultats du vote majoritaire ne représentent pas ce que le peuple veut, car ces résultats peuvent être aussi incohérents que si le peuple était irrationnel. Cette découverte remonte à Condorcet, un philosophe et mathématicien du XVIIIe siècle.
Depuis, la preuve mathématique a été renforcée. C’est le fameux « paradoxe de Condorcet » (ou paradoxe du vote).
À titre d’illustration, considérons un électorat composé de trois électeurs, identifiés comme 1, 2 et 3 et trois politiques publiques, X, Y et Z (par exemple, une subvention à l’emploi, une augmentation des allocations familiales et un salaire minimum plus élevé). Le tableau 1 décrit les préférences hypothétiques de nos trois électeurs.
L’électeur 1 préfère X à Y et Y à Z. On peut représenter l’ordre de ses préférences par « X Y Z ». Si cet électeur est cohérent ou rationnel, il préfère X à Z ; autrement dit, ses préférences sont transitives. Les préférences des électeurs 2 et 3 diffèrent, mais elles demeurent transitives.
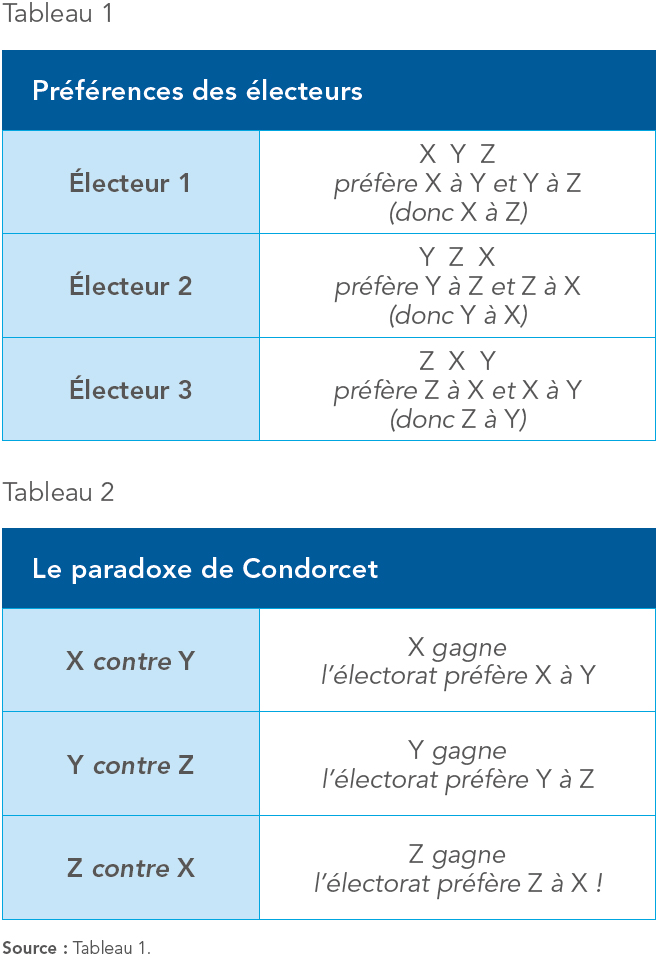
Supposons qu’un scrutin demande à nos trois électeurs de choisir entre X et Y. Étant données leurs préférences, il est évident que X l’emportera avec les deux tiers des voix puisque l’électeur 1 et l’électeur 3 préfèrent X à Y (Tableau 2). De la même manière, s’il faut choisir entre Y et Z (peut-être lors d’un scrutin ultérieur), Y l’emportera. Mais si le scrutin oppose Z et X, c’est Z qui gagnera. L’électorat préfère à la fois X à Z (une implication des deux premiers scrutins, en raison de la propriété de transitivité) et Z à X – une contradiction évidente.
Bien que chaque électeur individuel soit rationnel, l’addition ou agrégation des votes ne l’est pas. La majorité produira un cycle incohérent même si aucun électeur ne change d’idée. Impossible donc de savoir ce que veut « le peuple ». « Le peuple » n’existe pas comme décideur rationnel.
Si on modifie les préférences hypothétiques des trois électeurs, certaines configurations éviteront le paradoxe de Condorcet. Cependant, plus il y a d’électeurs, plus la probabilité est grande que le paradoxe affecte les résultats du vote.
Une confirmation empirique de ce phénomène a été observée durant une courte période de sept jours en janvier 1925.
Alors qu’un seul sénateur avait changé d’idée (ou avait fait preuve d’incohérence), le Sénat américain vota le renvoi d’un projet hydro-électrique à une commission d’études (X) au lieu d’autoriser sa réalisation par l’entreprise privée (Y). La réalisation privée (Y) au lieu de la nationalisation (Z). Et enfin, de manière incohérente, la nationalisation (Z) au lieu du renvoi à un groupe d’études (X)(2).
On ne s’étonnerait donc pas que, selon le mot d’esprit, l’électorat québécois ait voulu (voire favorise encore) « un Québec indépendant dans un Canada uni », même si les préférences de chacun des électeurs étaient cohérentes.
On doit une découverte majeure à Kenneth Arrow, alors à l’Université Stanford, qui démontra mathématiquement que le paradoxe de Condorcet affecte toutes les formes de scrutin qui respectent un petit nombre d’axiomes simples – notamment la transitivité des préférences individuelles, l’absence de dictature, et la non-dépendance vis-à-vis des options non pertinentes(3). Nos citations font référence aux ouvrages originaux en langue anglaise même quand des traductions françaises sont disponibles.]. Il obtint plus tard un prix Nobel d’économie. Pour simplifier, le « théorème d’impossibilité d’Arrow » démontre que le résultat d’un scrutin est soit irrationnel (comme dans le paradoxe de Condorcet), soit dictatorial au sens où les préférences d’un individu l’emportent sur celles des autres.
Donc, le peuple est incapable de gouverner. Ou bien c’est un peuple irrationnel qui gouverne, ou bien c’est un dictateur (de droite ou de gauche), lequel prétend incarner la volonté du peuple. Pour nourrir l’illusion d’un peuple uni, le leader populiste doit dénicher des « ennemis du peuple » qui sont exclus du peuple qu’il prétend représenter. L’histoire fournit de nombreux exemples(4).
Il existe d’autres problèmes. Différentes méthodes de scrutin sont susceptibles de produire des résultats différents. Le contrôle de l’agenda politique, c’est-à-dire des options proposées aux électeurs, change aussi les résultats.
L’UTILITÉ DE LA DÉMOCRATIE ET SES LIENS AVEC LE POPULISME
Le populisme serait plausible si on le définit comme un régime politique où, dans toute la mesure du possible, chaque citoyen individuel se gouverne lui-même – littéralement le self-government. Cependant, il existe déjà un label associé à cette philosophie politique, à savoir le libéralisme classique, représenté par les théoriciens de l’État limité comme Adam Smith, Jean-Baptiste Say, Milton Friedman, Friedrich Hayek, James Buchanan et plusieurs autres(5).
Dans son acception courante et historique, le populisme représente une corruption de la démocratie. La démocratie constitue un bon moyen pour changer les gouvernants, mais elle ne nous dit rien sur la volonté du peuple. Elle révèle seulement si une majorité, celle du moment, est satisfaite ou non du gouvernement actuel. Cela est déjà bien utile et correspond à la démocratie qui est possible dans la réalité(6).
Pierre Lemieux is an Economist affiliated with the Department of Management Sciences of the Université du Québec en Outaouais and a Senior Fellow at the MEI. He is the author of “Is Populism Possible?” and the views reflected in this opinion piece are his own.
Notes
- William H. Riker, Liberalism against Populism: A Confrontation between the Theory of Democracy and the Theory of Social Choice, Waveland Press, 1982 et 1988 ; Pierre Lemieux, « Populist Political Choices Are Meaningless », Regulation, vol. 44, no 1, 2021, p. 54-57.
- John N. Neufeld et al., « A Paradox of Voting: Cyclical Majorities and the Case of Muscle Shoals », Political Research Quarterly, vol. 47, no 2, juin 1994, p. 427-433.
- Kenneth J. Arrow, Social Choice and Individual Values, 2e édition,Yale University Press, 1963 première édition 1951
- Par exemple, voir Carlos de la Torre, Populisms : A Quick Immersion, Tibidabo, 2019.
- Pierre Lemieux, « The Impossibility of Populism », The Independent Review, vol. 26, no 1, 2021, p. 22-24.
- La vaste littérature scientifique sur ce sujet comprend notamment William H. Riker, op. cit., note 1; et F.A. Hayek, Law, Legislation and Liberty, vol. 3: The Political Order of a Free People, University of Chicago Press, 1979.

